考研高等数学知识点：反常积分

      反常积分是高等数学中的一个重要概念，主要分为两类：无穷积分和瑕积分。在考研高等数学中，反常积分的理解和运用是考试的重点之一。下面简要介绍反常积分的相关知识点：

　　瑕点与瑕积分：

　　瑕点：如果函数f(x)f(x)在点aa的任一邻域内都无界，那么点aa称为函数f(x)f(x)的瑕点(无界间断点)。

　　瑕积分：存在瑕点时，积分可能没有意义，或者极限形式不。瑕积分通常分为两类：类瑕积分和第二类瑕积分。

　　无穷积分：

　　无穷积分指的是当积分区间趋向于某一值时，积分的值趋向于无穷大。

　　无穷积分的判别法包括：

　　比较检验：比较被积函数与

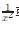
     或其他特定函数的增长速度。

　　夹逼定理：如果被积函数在区间[a, b]上单调减少，并且被积函数在a处有界，在b处收敛到某个值，则无穷积分存在。

　　瑕积分的计算：

　　类瑕积分的计算通常涉及部分和公比级数的方法。

　　第二类瑕积分的计算一般采用解析延拓的方法，通过引入一种意义上的积分，使得原本无意义的积分变得有意义。

　　重要性质与定理：

　　柯西积分定理和柯西积分公式在处理瑕积分问题时非常重要。

　　积分限的变换也是处理反常积分问题的一个有效方法，如牛顿-莱布尼茨公式、换元积分法、分部积分法等。

　　在考研复习中，反常积分的掌握需要通过大量的练习来提高。建议使用历年考研真题进行训练，同时参考一些高质量的辅导书籍和课程，如武忠祥老师的高数每日一题等，这些都能帮助你更好地理解和运用反常积分的相关知识。

　新航道-用心用情用力做教育!

　　>>点击在线咨询<<

　　400-900-9767