当前位置：首页 > 锦秋A-Level频道 > A-level > 21年1月考试季锦秋师资考点解析|A-Level数学P1-4考情回顾及备考指导
发布时间：2021-03-10 关键词：
摘要：申请英国院校理科专业的同学们肯定都知道A-Level数学在整个A-Level课程中的重要性，整体来看国内高中数学的知识范围比A-Level要窄，A-Level数学涉及的知识面很宽，
申请英国院校理科专业的同学们肯定都知道A-Level数学在整个A-Level课程中的重要性，整体来看国内高中数学的知识范围比A-Level要窄，A-Level数学涉及的知识面很宽，比如纯数部分涉及到简单的微分方程求解、积分的应用等，这些都是在国内大学才会接触的知识下面我们一起跟着锦秋数学组老师回顾下爱德思考试局2021年1月考试季A-Level数学考情解析!
锦秋师资带你梳理考点啦!!
A-Level数学P1
2021年1月考情分析
考试日期：2021年1月11日
考试时长：1小时30分
01
本题考查第8章differentiation有关导数求解、导数的图像意义及应用等考点。须通过导数求得原函数在垂足处的斜率后，再根据垂线与原函数斜率关系求得垂线方程。可直接套用书上公式，属于常规问题。
02
与2019年10月份官考第2题神似，主要考查考生基本的方程求解能力以及应用题读题理解能力。只需将两组x、y值代入方程求解参数即可，属于简单题。
03
本题考查图像变换以及三角函数图像，与2020年1月份官考第7题神似。
a问)对cosine函数图像进行了stretching变形，已知变形过程，求变形结果。
b问)在a问的基础上进行了translation变形，已知变动结果，反推变形过程。本题需要学生对三角函数图像的精确记忆，以及函数图像变换相关知识的熟练掌握。
04
本题考查知识点较多，包括straight line、quadratics以及inequalities的相关内容。
a问)已知两点坐标求过两点直线解析式，直接代公式求解即可。
b问)已知抛物线顶点和线上另一点坐标，求抛物线解析式，可以通过抛物线顶点坐标公式或对称轴坐标公式直接解方程组得到答案。
c问)考查不等式组的几何意义，列出正确不等式来定义阴影区域。本题综合性较强，考点属于常见类型。
05
本题是对radians、trigonometric ratio相关内容的考查。需要学生熟练运用sector面积公式、triangle面积公式、sine rule以及length of arc公式。其中第a问采用sine rule求未知角时应注意角度取值(钝角而非锐角)。
06
本题考查了第4章的反比例函数图像及图像转换，已知两条曲线解析式交点个数、以及二次不等式的求解。
a、b问)要求画出stretching、translation变换后的反比例函数图像，并标出渐近线和与坐标轴交点。
c问)可通过联立解析式，并令discriminant小于0，通过求解二次不等式来求解参数k的取值范围。本题亦比较综合，知识点较多。
07
本题主要考查方程求解以及一阶导、二阶导等考点。
a问)可采用换元法，将
看作一个未知量，从而将原方程转换为一元二次方程求解。
b问)求解二阶导，属于微分计算最基本操作。
08
本题考查三次函数解析式及图像以及二次函数求解。问法比较灵活，需要学生对解析式及相应图像理解透彻，并熟练运用。本题基本上都在因式分解和脱括号，比较考验基本功，只要能正确理解题目意图，并保证计算不出错，本题不难得分。
09
本题考查积分的计算。
a问)学生需要用到第1章index law的部分知识对函数式进行化简变形，然后求不定积分。
b问)解带参数的函数关系式，需要根据题目中给出的关系条件，列多个方程形成方程组并求解。本题比较常规，主要考查计算。
小结
总体来说，本次考试难度依然保持稳定，多个题目与之前的真题相近或神似。与上次考试一样，本次试卷中与函数图像和图像变换相关的题目依然较多，其中直接考查图像的问题达到10分以上，其他题目通过图像提问或表示的亦不在少数，由此可以看出，深刻理解函数与其图像的联系在本单元考试中显得较为关键。另外，本次考试中与带参数的表达式相关的问题略多，需要通过方程组求解，这种稍显抽象的题目更要求对知识点的灵活掌握。
A-Level数学P2
2021年1月考情分析
考试日期：2021年1月18日
考试时长：1小时30分
01
本题考查P2第1章因式定理，余数定理。是普通常规的题目，分别运用因式定理和余数定理列出方程组，联立就可以求出未知数。
类似真题：
June 2019 Q6，Nov 2019 Q4，Jan 2020 Q3a， Oct 2020 Q3
02
本题考查P2第7章微分的知识点，小问运用一次微分等于零来求极值，第二小问通过对函数进行二次微分来判断上一问求得的是值还是最小值，这道题目是很常规的题目没有任何变化。
类似真题：
Nov 2019 Q1，Jan 2020 Q10
03
本题考查P2第3章指数对数函数的知识点。问是把给的指数函数转换成固定对数函数的形式，需要用到指数的运算法则(同底数指数相加变成同底相乘)进行转换，并且求解。第二问是常规的解对数函数方程，需要注意的是解完方程之后y的值的取舍。
类似真题：
June 2019 Q8，Nov 2019 Q7， Jan 2020 Q9，Oct 2020 Q9
04
本题考查P2第4章二项式展开，小问要求按照x的升序次方写出前三项。此题属于常规题型，常规考查，第二小问需要用给的多项式与上一问展开的式子相乘找到二次项前面的系数。
类似真题：
June 2019 Q4，Nov 2019 Q3， Jan 2020 Q2，Oct 2020 Q1
05
本题考查P2第1章证明题的知识点。小问考察的是倒推法，第二小问是反例法。证明题近几次考试都没有出现，上一次出现是在2019年6月，此次证明题考查的题目难度基本与课本课后题目持平。
类似真题：
June 2019 Q3
06
本题考查P2第6章三角函数的知识点。小问是三角函数的转换，基础，只需要记住基础的三角函数的公式就可以推出;第二小问是运用上一问的结论直接运用ASTC和计算器求三角函数的转角，单位要用弧度制并且保留三位小数位。
类似真题：
June 2019 Q9，Nov 2019 Q9， Jan 2020 Q7，Oct 2020 Q7
07
本题考查P2第8章梯形法则，小问常规题目根据x求y的值，需要注意答案要保留四个有效数字;第二小问则是直接套用梯形法则公式求面积，答案要保留二位小数。
类似真题：
Jan 2020 Q1，Oct 2020 Q2
08
本题考查P2第5章数列的知识点。小问是根据递推关系公式写出数列的第二项，第二小问则是根据求和符号直接对前三项求和，列出前三项相加即可得出等式求出未知数P，之后再代入P求得第二项。
类似真题：
June 2019 Q1
09
本题考查P2第2章圆的方程。A问的两小问常规题目，求圆的圆心半径以及方程;B问证明点在圆上，直接代入即可求出未知数K;C问根据圆的切线垂直于圆心到切点求出圆上一点的切线方程，之后再根据方程求出与x轴交点，之后就可以直接求出三角形的面积。
类似真题：
June 2019 Q2，Nov 2019 Q6，Jan 2020 Q6，Oct 2020 Q4
10
本题考查P2第5章等差等比数列的知识点。A问考察的是等差数列的通项公式;B问考察的是等比数列的通项公式;C问考察的是等差等比数列求和公式，需要注意最后求完x要保留整数。
类似真题：
June 2019 Q7， Jan 2020 Q8，Oct 2020 Q5
小结
本次P2考试较为简单，计算量不大，问题都很直接，没有需要技巧的新题，考察的题目基本涵盖了整个P2的知识点。此次考试没有考察到多项式的除法;递增函数，递减函数的斜率以及定积分求不规则图形的面积。
此次考题，数列的题目考察的较多，占比24%，其中等差和等比的知识点以及递推关系公式求和都考察到了，余下的题目往次考察的重点微积分和三角函数在这套题目中只占比28%，并且计算量大的容易出错的定积分求面积题型还没有出现。
总而言之，这一套题目整体难度不高，算是考试局给出的福利。
A-Level数学P3
2021年1月考情分析
考试日期：2021年1月14日
考试时长：1小时30分
01
本题考查了P3的第7章积分。考生需要先将原式化简成两个式子相减的形式，然后利用积分的基本公式求出最后的答案。在应用公式的时候需要注意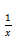
和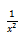
的公式不一样;不定积分记得在最后加常数C。
类似真题：
2020 Jan Q8
02
本题考查了P3的第2章图像变换。题目给出原函数的图像，要求考生按照题目要求画出变化后的图像，并且标出图像和y轴的交点以及maximum/minimum turning point。
(i)问考查了水平和竖直方向的拉伸，因为方向不同所以顺序不受影响，分两步考虑就可以了。
(ii)问考查对称和平移的综合变换，方向依旧不同，所以难度不大。
03
本题考查了P3的第1章分式四则运算和第2章反函数。
a问)运用分式的四则运算将题目所给式子进行化简。运算是需要先化简后运算，先将分母进行因式分解，再进行通分运算。
b问)求分式函数的反函数。
c问)求反函数的domain即原函数的range。
类似真题：
2020 Jan Q2
04
本题考查了P3的第2章值函数及其图像，解值方程。
a问)求值函数的最小值，因为值为非负数，所以当值内的数值为零时，函数整体取到最小值。
b问)考查值函数的画图，因为是整体加值，作图时分两步：1.画出原函数图像，2.将x轴下方的图像对称到x轴上方，x轴上方的图像保持原样。
c问)解值方程，考生需要根据实际情况或者图像去掉值符号解出答案，最后注意验根并舍去增根。
类似真题：
2020 Jan Q6，2020 Oct Q4
05
本题考查了P3的第5章指数函数和第6章求微分。
a问)根据题目给出的初始条件求出未知常数A的值。
b问)进一步给出条件，求出k的精确值。
c问)求当t=9的时候，烤箱内的温度。考生将t值代入，剩下的交给计算器就好了。
d问)求t=9时温度的变化率。找出关键词“rate of increase of the temperature” 联系到需要求微分，并代入t=9。
类似真题：
2020 Jan Q1
06
本题综合考查了P3的第6章微分和第7章迭代方程。
a问)用过product rule求函数的微分。
b问)令微分等于零，将所得式子化简成题目要求的形式，这里用到了反三角函数，考试的时候要写成题目要求的“arctan”而不是。
c问)以上一问的式子做为迭代方程求的值。最后一问，证明在保留3位小数时，微分等于零时题目所给的数值。常规考点，做题时需要注意用计算器的时候不要手滑，单位是弧度制。
类似真题：
2020 Jan Q7，2020 Oct Q6
07
本题考查了P3的第3章三角函数，第4章两角和差及二倍角公式。
a问)证明式子左右两边恒等。通过观察发现左侧既有单角又有倍角而右侧只有单角且形式简单，所以我们从左侧入手，利用二倍角公式将左侧展开并化简成右侧的形式。
b问)根据上一问的结果解出符合条件的值。部分考生对于三角函数的证明不是很熟练，往往耗时长，做不对。造成整个大题都没有做出来。考试的时候如果问比较困难，可以直接借用上一问的结果继续完成答题。
类似真题：
2020 Jan Q5，2020 Oct Q1
08
本题考查了P3的第5章指数函数化曲为直。这道题本身难度不大，但是整个题没有图像，只有文字描述，对于英语阅读不是太熟练的考生可能英语的考验远大于数学的困难，同学们在平时的学习中要注意英语的。
a问)已知直线斜率和与y轴的交点，求常数a，b的值。
b问)解释上一问中常数a所表示的意义。c问用所有模型预测2015年的“percentage of population”。
类似真题：
2020 Jan Q3，2020 Oct Q2
09
本题考查了P3的第7章：积分--reverse chain rule。两问分别对应了两种standard pattern，在判断出可用的公式后直接代入，并且调整系数就可以了。难度不大，而且不需要计算。
10
本题考查了P3 的第6章微分—chain rule。
a问)给出x的表达式，求dx/dy，分清自变量和因变量，运用链式法则求微分即可。
b问)求dy/dx，在化简的时候需要用到三角函数的恒等式。c问求函数的法线方程，将答案写成的形式。
类似真题：
2020 Oct Q8
小结
本次P3考试较为简单，难度相比2020年10月的P3考试有所降低。三角函数和微积分部分题目都不是太难，尤其是积分部分，考查的都是不定积分，像是指数的化简，对数的化简等都不会用到。积分中难度较大的trigonometric identities没有涉及。
另外往年必出的辅助角公式也没有考到。虽然有10道题，感觉题量较大，但是难度都不是太高，以常规题为主，和平时所学所练的内容出入不大，平时踏实练习，认真总结的学生会容易取得，善于攻克难题但容易粗心的同学无法拉开差距。
A-Level数学P4
2021年1月考情分析
考试日期：2021年1月07日
考试时长：1小时30分
01
本题考查了P4的第4章二项式展开。
a问)常规题，先将常数项化成1，然后利用二项式展开的公式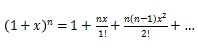
将式子写成多项式的形式，或者可以直接套用
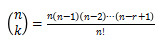
将题目所给式子直接展开。题目要求写前四项，所以答案需要写成
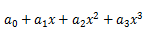
的形式。
b问)借助a问的结果算出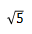
的近似值，这是二项式展开的常考题型，答题时需注意直接代入时所得到的是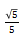
的值，要得到最后答案应该乘以5。
类似真题：
Oct 2020 Q2
02
本题考查了P4的第7章向量。
a问)求两个向量所形成的夹角度数。需要注意两个细节：一个两个向量的方向，需要保持一致，同时指向一个点或者同时从一个点出发;第二个是单位，题目要求角度制。
b问)求平行四边形的面积，使用P1的公式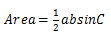
求出三角形的面积，然后再乘以2。
03
本题考查了P4的第1章证明。这道题是课本上例题的原题，要求考生用反证法证明：没有的奇数。在官考中出现课本上的例题是罕见的，所以这道题分值不高，只有2分。只要好好准备，这道题拿满分不成问题。
04
本题考查了P4的第5章参数方程。
a问)已知函数的参数方程表达，求函数的笛卡尔方程。考生可以采用代入法，用含有x的式子表达t，然后再代入y 中，化简成关于x的式子。方法不难，主要是化简的时候需要用到P3分式化简的知识，考生注意不要自己发明化简的法则。
b问)是P3的一个知识点：函数的值域，考生需要能够求根据a问的domain求出函数的range。
05
本题考查了P4的第6章积分。这道题需要考生用换元的方法求积分的精确值，并且将答案写成题目要求的形式。需要注意在计算定积分时不要忘记替换limit。题目直白，难度不大。
06
本题考查了P4的第5章隐函数求导。
a问)用x和y表达出dy/dx。
b问)先求函数和y轴的交点，然后求出过该点的法线方程。这是隐函数的常规考法，以往的试卷和课后题都有较多的相同类型的题目。需要注意的是求导过程中chain rule和product rule的使用。
07
本题考查了P4第6章积分的内容。
a问)考查了分部积分。这是课本例题的一个变形，主要是在分部积分的过程中，积分主体重复出现，考生需要将要求的积分看作一个整体进行计算。
b问)求函数和x轴所围成的面积。先求出函数和x轴的交点作为upper and lower limit，然后代入上问求出的积分中，就能得到题目要求的形式。
08
本题考查了P4第7章向量。本次考试的第二道向量题，难度也不大。证明两条直线是异面的关系。通过x和y坐标相等求出λ和μ的值，然后代入z坐标即可。
09
本题考查了P4的第6章积分。考生需要求参数方程围绕x轴旋转360°之后所围成的图形的体积，利用公式
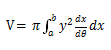
得出最后的结果，并将结果的精确值用题目所要求的形式写出来。首先考生需要先通过三角求出函数图像和x轴的交点，然后利用三角函数的恒等公式证明出a问要求的式子。b问在上一问的基础上求出积分的精确值。本题积分的解法难度不是太大。
10
本题考查了P4第6章积分，微分方程的内容。以应用题的形式，题目表达不是很难。没有和相关变化率的知识一起考查，从程度上降低了难度。
a问)考查partial fraction，难度不大，为后面做铺垫。
b问)题目给出微分方程以及初始条件，学生可以采用分离变量法证明出H的表达式。
c问)需要求出当H=8的时候，t的值是多少，可以代入到上一问求出的式子中。
d问)需要求出H的表达式的limit，这个是P3的一个常考点，分式函数的range。
类似真题：
Oct 2020 Q9
小结
本次P4考试较为简单，难度相比2020年10月的P4考试有所降低。微分和积分仍然是考查重难点，但是计算量不大，问题都很直接，没有需要技巧的新题。平时授课和练习过程中，学生掌握不是很牢固的证明题本次考试竟然出了课本的例题，并且分值只有两分，这在以往的考试中是没有出现过的，相信在今后的考试中也不太有可能再次出现。还有向量部分，很久没有出现的求平行四边形的面积的题目又“重出江湖”，披着P4的外衣实则考的是P1的知识点。
考试难度不大，更加需要注意做题的规范性和计算的准确，避免在不必要的地方丢分，从而与A*失之交臂。
