21年1月考试季锦秋师资考点解析|A-Level数学M1-3考情回顾及备考指导

　   中国学生的数学水平在世界都是有名的留学的宝宝纷纷发挥中华民族的“数学基因”将选科必选数学发扬光大，于是好奇的同学就问了都说A-Level的数学比高考数学简单是这样吗?A-Level的数学包括基础数学和进阶数学在内容上基础数学和进阶数学有连续性，但这是A-Level的两门独立课程，学生可以单独选择其中一门，但中国学生一般会都选数学的教学内容有四大模块：纯数学(pure mathematics)、统计数学(statistics)、机械数学(mechanics)、决策数学(decision mathematics)，下面我们一起跟着锦秋数学组老师回顾下爱德思考试局2021年1月考试季A-Level数学考情解析!

　　锦秋师资带你梳理考点啦!!

　　A-Level数学M1 2021年1月考情分析

　　考试日期：2021年1月19日

　　考试时长：1小时30分

　　01、考查匀加速直线运动

　　(a)题目中提供了初速度u的信息，另外重力加速度g取9.8。抛射点距离地面5米而目标点是距离地面2m的位置，所以位移是向下的3m。代入公式2as=v2-u2即可求得末速度的大小。当我们规定正方向为向上的时候，初速度为正数，加速度和位移都为负数。

　　(b)当落地的时候位移为向下的5m。使用公式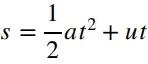

　　，规定正方向向上，其中初速度为20m/s，加速度为-9.8m/s2，而位移为-5m，求解时间t即可，t有两个解，我们保留正数解舍弃负数解。

　　02、考查动量守恒

　　碰撞中受到的量方向应该跟受力方向一致，规定沿着P初始速度的方向为正，则有

　　(a)P受到的量与自己的速度方向相反，为负数，根据量的定义，-5mu=Pf - (6mu)，可以解得P的末动量为mu，由于P的质量为2m，所以P的末速度为0.5u，方向与初始方向相同。

　　(b)Q受到的量与自己的速度方向相反，由于Q的速度方向与我们规定的正方向相反，所以量为正数，5mu=Pf - (-2mu)，解得末动量为3mu，所以末速度为3u方向与Q的初始方向相反。

　　03、考查力的平衡

　　对于平衡问题来讲，质点在各个方向所受到的合外力为0。由于题目要求的是拉力T的最小值，当拉力T较小的时候，物体因200N的力有向左运动的趋势，所以摩擦力f的方向向右。根据水平方向的受力平衡可得200 cos15=f +T cos25，垂直方向为200 sin15+Tsin25+R=mg。最后，由于是极限的平衡状态f =μR，求解方程组即可得到答案。

　　04、考查力矩平衡

　　题目描述了两种情况，在种情况中，杆有关于D点翻转的趋势，此时支撑点C的力为0，根据力矩平衡，关于D点求力矩，可以列出等式W(6-x-1)=900(6-1)。在第二种情况中，杆有关于C点翻转的趋势，此时支撑点D的力为0，根据力矩平衡，关于C点求力矩，可以列出新的平衡要求W(x-1)=1500 x 5。联立方程组求解可得到W和x的值。

　　05、考查向量的合成

　　方向角为正北方出发顺时针扫过的角度，建立坐标系，规定i轴正方向朝东，j轴正方向往北，则可以将题目中描述的向量F和G进行分解，可得F=8cos240i + 8sin240j，而G=-10j。那么求和之后R=8cos240i +(8sin240-10)j。

　　(a)R的大小可以通过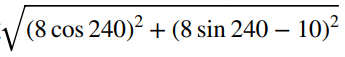进行计算。进行计算。

　　(b)通过画图可知R的方向指向左下，其跟j轴负方向的夹角可以通过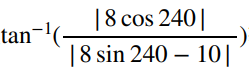

　　获得，最后再加上180度即可得到方向角的解。

　　06、考查平面运动

　　(a)根据匀速运动在平面内的表达式可以求解：rA=rA0 +vAt =(11+3t)i +(11-t)j。

　　(b)在时刻t=6，rA=29i+5j，对于B来讲，其位移可以表达为RB=(7+4t)i+(16-2t)j，当两者i坐标相等时，可以解得t=5.5，当两者j坐标相等时，可以解的t=5.5。

　　(c)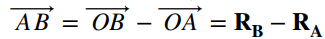

　　，代入前面计算的结果即可得证。

　　(d)两者的距离的平方可以表达为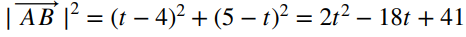

　　。求解该二次函数的极小值再开根号即可得到最近的距离的值。

　　07、考查运动学图像

　　(a)根据匀加速直线运动的公式v=u+at，代入数值求解即可。

　　(b)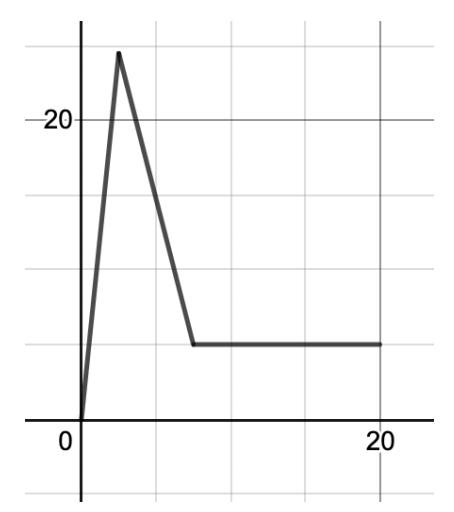

　　(c)对于减速的部分使用匀加速直线运动的公式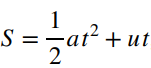

　　，规定向下为正，其中初速度u为段运动到达的末速度，加速度为-3.9ms-2，位移为73.75m。

　　(d)求解整个图形的面积之和即可。

　　08、考查链接体

　　(a)假设绳子上的拉力为T，加速度为a，则对于A可以分析得到T-mAg sinα-f=mAa，其中摩擦力f=μR，而支持力可以通过mAg cosα=R得到。对于B分析可以得到mBg-T=mBa。联立方程组求解即可。

　　(b)当A和B走过了共同的h距离之后，B因为撞击而立刻停止，拉力消失，A则会因为摩擦力和重力的分量而减速，减速度可以通过mAg sinα+f=mAa来计算。利用公式2as=v2-u2计算上一个运动产生的末速度之后，可以计算得到减速部分走过的位移，再加上h即可得到d的最小值。

　　(c)滑轮上可能有摩擦力。

　　#FormatImgID_6#

　　A-Level数学M2 2021年1月考情分析

　　#FormatImgID_7#

　　考试日期：2021年1月12日

　　考试时长：1小时30分

　　01、第五章：量和向量的计算问题，主要考查学生对量的向量性质的理解和向量的计算。类似问题并不少见，多加注意就并不困难。

　　02、第三章：质心与悬挂的问题。本题质心的求解十分简单，lamina是一等腰三角形，只需运用三角形求质心公式即可得到答案。

　　悬挂相对较少见。该lamina是在一水平外力的作用下保持平衡的，于是一般的质心处在悬挂点正下方的方式无法使用，必须使用力矩平衡进行计算。找lamina重力的力臂时需要用到相似三角形。

　　03、第四章：功率问题，P=Fv。

　　本题有两个未知数和两个车辆运动状态的条件，需要分别列出车辆的受力情况然后联立方程求出结果。

　　本题不是特别简单，但很常见。

　　04、第三章：质心与悬挂。这是本次试题中的第二道质心与悬挂问题。

　　需注意题目中是一个framework，好在其形状并不容易被误认为是lamina，所以因审题不清导致误判而出错应该不大可能。Framework的质心计算应运用每北京段的长度。

　　悬挂部分是一个基础和常见的问法，难度不高。

　　05、第二章：变加速运动，向量的积分与微分。

　　题中给出一速度向量，需要我们

　　a) 求出运动方向与某一向量平行的时刻。本问需要了解向量平行的计算;

　　b) 求加速度的大小，需要首先微分速度向量得到加速度向量，再代数并求大小;

　　c) 求位置向量，需要首先积分速度向量得到位置向量，再进行代数。

　　本题比较常规，没有易错点，只需仔细读题并按部就班完成。

　　06、第六章：刚体的平衡。

　　有一斜搭在墙上的梯子有两种状态：当一人站在C点时，梯子平衡;当其移动到D点时，梯子依然平衡，但达到了极限平衡状态。本题ab两问即是分别提问这两种情况。需要注意的是，种状态并没有达到极限平衡，所以不能使用f=μR。

　　本题计算稍有难度，但并没有超出从前曾有过的水平。

　　但另有一c问，提问梯子是rod这一modelling assumption。这类文字题在M1中常考，虽然在M2中也同样运用了相同的modelling assumption，但从没有出现过，所以也许一些同学已经遗忘了。

　　07、章：斜抛;第四章：能量。

　　本题是一斜抛问题，可用水平竖直方向分开进行运动计算的方式解答。但其中问明确要求必须使用能量的方法，那么就需要使用机械能守恒来计算小球抛起和落地时的状态。

　　后两问分别提问了滞空过程中的最小速率和速率大于10m/s的滞空时间，都是常见的抛物运动问题。

　　08、第五章：碰撞与回复系数。

　　a) 计算回复系数e。两个初速度都未知，通过给出量的大小而使其可以计算。这里要注意判断清楚量的方向和正方向，以确保初速度的计算正确。

　　b) 一球在碰撞后撞墙，又反弹回来和另一球第二次碰撞，求第二次碰撞的位置。本问计算原理简单，只需一个s=vt的公式，但步骤对于一些同学可能有些复杂，容易出错。相对来说是一个难度较高的小问，但前几年曾有过几乎一样的问题，并不新奇。

　　A-Level数学M3 2021年1月考情分析

　　考试日期：2021年1月14日

　　考试时长：1小时30分

　　01、(a) 考点是利用积分求旋转体的体积，直接套P4部分现成的公式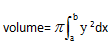

　　;

　　(b) 考点是利用积分求旋转体的质心，直接套现成的公式。

　　02、(a) 考点是万有引力的反平方规律F=k/x2，利用地球表面(x=R时)的万有引力为mg来求k。

　　(b) 考点是利用F=ma来列方程，然后积分求速度。解这类题目时，正负号容易出错，如果以远离地球球心为正方，则F应该是负的，因为是指向圆心的，学生容易忽略这一点。解这类题目，可以用a=vdv/dx分离变量求解，也可以用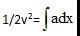

　　直接积分求解。

　　03、(a) 考点是圆周运动中的F=ma。水平方向列F=ma的方程，竖直方向列平衡方程。这类题目，两个方程所分析的方向必须是垂直的，否则两个方程不独立。

　　(b)

　　04、(a) 考点是复合的质心的求法。首先需要注意的是，这里的研究对象是solid，而非shell。其次，本题可以认作是从一个大的solid cone里扣除掉了两个小的solid cone，化简为了典型的求复合质心的题目。

　　(b) 考点是求悬挂物体时形成的夹角。解此类问题，先连接悬挂点和质心，来确定downward vertical line，然后再根据质心的坐标来求角度。因为A点，B点和质心三个点的坐标都是已知的，所以，可以借助P4中向量的知识来求夹角,即，套用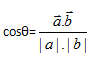

　　05、(a) 考点是胡克定律(Hooke’s law)，列一个力的平衡方程，再列一个total extension=4a的方程，联立求解即可。

　　(b) 考点是证明S.H.M。此类题目是必考题，套路固定。先令particle处于某个距离平衡点距离为x的位置，再列F=ma的方程，最后凑成

　　的形式即可。学生容易忽略步，导致最终结果里没有x的出现。

　　(c) 考点是v2=ω2(a2-x2)。这里一个容易犯的错误是，学生会直接把7a/2认为是x，实际上是不对的。x应该是距离平衡点的位移，所以在这里应该是0.5a。

　　06、(a) 考点是能量守恒和圆周运动。首先，列从A点到顶点的能量守恒的方程，求出在定点处的速度;再根据求出的速度，列F=ma的方程，求顶点处绳子的拉力T。要证明“complete vertical circles”，只需要求出T大于0即可。

　　(b) 考点同(a)，这里要注意的是，当particle处于点时，绳子的拉力是的。所以，只需要求出particle处于点时绳子的拉力，并且小于7mg即可。

　　07、(a) 考点是能量守恒。利用Energy lost-μRx=Energy gained列方程即可。

　　(b) 考点是胡克定律和摩擦力。当particle处于A点时，会受到沿斜面向下的Tension和component of weight，以及组织particle滑动的μR.。如果前两者的和大于第三者，则，会滑动。

　　总评

　　难度不大，所有题目都比较常规和典型，比前两次官考的题目要简单一些。