A-Level物理学生必知的最美物理学实验的创造者——密立根

       罗伯特.密立根是著 名的美国实验物理学家，1923年诺贝尔物理学奖得主。1910-1917年曾以油滴实验精确地测得了基本电荷的电荷量的值，从而确定了电荷的不连续性。1916年曾验证了爱因斯坦的光电效应公式，并测定了普朗克常数。在这篇文章中，我们将介绍这两个重要的实验。

　　一、油滴测量基本电荷的电荷量

　　在20世纪初，物理学家对于电荷是否连续产生了争论，一部分科学家认为电荷是连续的，就如一般意义上我们理解时间或者长度一样，可以无限进行细分;但是另一部分科学家认为电荷是离散的，存在有一个不可进一步细分的基本电荷量。围绕着这个争论，密立根和哈维.弗莱彻设计了一个实验来对这两种理论进行检验。

　　实验的设计(图1.)简化版本如下图所示：

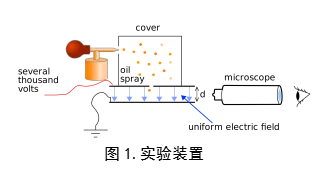
　　总体来讲，其流程可以概括为利用带电粒子在电场中受力的特性，用已知的电场强度推算带电物体的电荷量，再通过寻找不同的电荷量之间的关系来发现他们是否连续。下面让我们来详细的介绍整个的实验流程。

　　之所以叫做油滴实验，因为第 一步我们需要利用一个特定的装置(图2.)制造油滴。

　　这里的油滴并不是一般意义上我们认为的那种从壶里面倒出来的一整滴，而应该是类似于一个喷雾装置喷出的雾中的一个小液滴，其体积是非常非常之小的。在喷出的过程中，由于跟喷嘴的摩擦，部分油滴就有可能带上电荷，当然，也可以使用X光照射这些油滴使它们带上电。

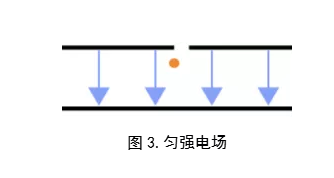
　　之后我们需要让这些带电油滴降落到一个匀强电场(图3.)的环境中，由于油滴带电，在匀强电场中油滴会受到力的作用，假如两平行极板之间的距离是定值，电势差可以调节，那么根据公式

　　我们就可以调节匀强电场的电场强度E。对于一个电荷量为q的粒子，在一个电场强度为E的匀强电场中，其受力可以通过公式F=qE来进行计算。而又因为在电场中的油滴只受到重力和电场力的作用，所以如果这两个力大小相等方向相反，那么油滴受到的合外力就会变成0，油滴就可以静止在匀强电场中。也就是说，对于一个处于平衡状态的油滴来讲，我们总是有

　　其中重力加速度g，两极板之间的电势差V和两极板之间的距离d都是可以直接得到的，也就意味着只要我们可以得到油滴质量m，那么就可以利用上面的公式计算出油滴上面的电荷量q。

　　在实际操作这个实验的时候，油滴质量m的测量是一个比较困难的点。在当时并没有能够直接精确测量的方法。所以油滴的质量最终需要通过公式

　　来进行计算，其中为油的密度ρ，V是油滴的体积，而又因为这个极小的油滴以球形存在，所以体积又可以通过球的相关公式，使用半径r 计算得到。那么究竟如何可以确定油滴的半径呢?直接测量是不现实的，一方面是油滴极小，直接测量会产生比较大的百分比不确定性;另一方面则是油滴的形状一旦受到测量仪器的外力影响就无法维持。所以这里采用了一个非常巧妙的方法来完成对其半径的测量。

　　我们都知道，在流体中运动的物体会受到阻力的作用，如果流体的流动是平流(Laminar Flow)，那么阻力的大小就可以使用斯托克斯定理(Stokes’ Law)计算，即F=6πrηv。其中η为流体的粘滞系数，r是小球的半径，v是相对速度。由于物体在流体中下落的时候受到阻力，浮力和重力的三个力的作用，而阻力又会随着速度增加而增加，最终物体会达到一个受力平衡的匀速运动状态，这个最终的速度我们称之为终端速度(Terminal Velocity)，可以通过公式

　　来进行计算，其中ρs和ρf分别为小球和流体的密度。也就是说，如果我们让小油滴在空气中到达终端速度并测量出来这个速度，就可以利用上面公式推算油滴的半径了。

　　再经历了上面的计算过程之后，油滴上面携带的电荷量q也终于可以计算了，我们可以统计带有不同电荷量的油滴的个数，然后将这些信息体现在一张图像上(图4.)。

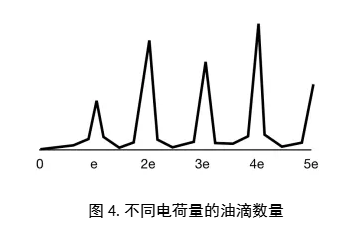
　　观察可以发现，在某些特定的电荷量上油滴的数量特别多，这就是电荷不连续的证据，对于一个油滴来讲，它只能拥有基本电荷的整数倍电荷。在经历了一系列精密的测量和计算之后，密立根得到了一个1.5924x10-19C的基本电荷量，这与现在被广泛接受的1.6022x10-19C的电荷量非常之接近了。

　　二、光电效应的实验

　　在爱因斯坦发表了关于光电效应的解释之后，这种将光同时理解成波和粒子的解释给了当时的科学家巨大的冲击，密立根对爱因斯坦的理论表示怀疑，所以他决定设计一个实验来验证爱因斯坦所提出来的这个理论。

　　所谓的光电效应就是特定频率的电磁波照射到金属板上时可以导致电子释放的现象，在传统的波的模型当中，由于能量是连续传递的，所以理论上无论什么频率的电磁波都可以将能量传递给金属板里面的电子，使得电子能够获得足够的能量以逃逸出金属板的表面，但是在现实的实验中，只有大于某个特定频率的电磁波才会导致电子释放。

　　爱因斯坦在解释光电效应的时候将光理解成粒子，也就是所谓的光子(Photon)，每一个光子所含有的能量可以通过公式E=hf来进行计算。当一束光照射到金属板表面的时候，金属板里面的电子可以吸收光子中的能量，如果吸收的能量大于了逃逸功Φ(即电子逃逸初金属板表面所需要的最小能量)，那么这些电子就可以逃逸出去(图5.)，而剩下的能量以动能的形式存在。

　　以上过程也可通过公式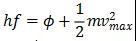

　　来进行描述。其中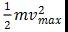

　　表示的就是电子在逃逸出金属板表面后所能够拥有的最 大动能。密立根的实验设计(图6.)包含一个真空管和一套相关电路。

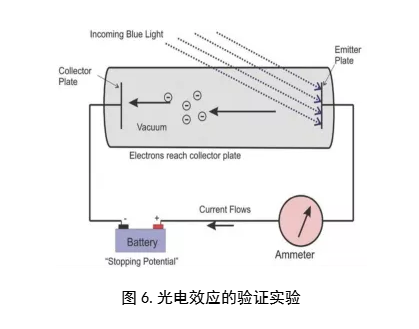
　　在真空管内部的阴极(Cathode，与电源负极相连的电极)和阳极(Anode，与电源正极相连的电极)之间的电势差可调，如果电磁波照射到阳极上并发生了光电效应，那么逃逸出来的电子就有可能会运动到阴极上，在电路中也就形成了电荷的定向运动—电流，电路中的电流表就是用来检测这种微弱电流产生与否的。但是，由于阳极和阴极之间的电势差，逃逸出来的电子会受到阻力的作用(电子的速度方向与电场线同向，但是电子的受力与电场线反向)。如果电子依然能够从阳极运动到阴极，那么电子的电势能增加量可以通过公式ΔU=eV来进行计算，其中为e电子的电荷量，V是阴极和阳极之间的电势差。如果逃逸出来的电子拥有足够的动能，这些动能就会部分转化成电势能，电子也就可以从阳极运动到阴极，而如果电子的动能不足，则没有办法运动到阴极，电路中也就不会形成电流。

　　在实验中，首先先通过电磁波的照射让阳极发生光电效应，电子逃逸出金属板的表面，之后从小到大调节阴极和阳极之间的电势差，在一个特定的电压上，电极之间的电势能等于电子的最 大动能，电流会突然消失，这样的电压我们称之为截止电压，用Vs来表示。即

　　在使用不同频率照射金属板的时候，使用不同的截止电压可以让电流消失，如果将最 大动能和频率之间的关系化成图像(图7.)，就可以得到一个线性关系。

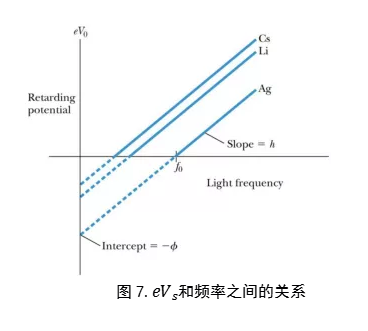
　　之所以是一个线性关系，是因为当我们将公式

　　中的

　　用eVs进行替换以后，公式可以改写成eVs=hf-Φ。所以在得到的直线图像中，其斜率为普朗克常数h，与y轴的截距则是负的逃逸功(-Φ)。也就意味着对于不同的金属，由于其逃逸功不同，所以直线与y轴的截距会有所差别，但是所有直线的斜率都是普朗克常数，所以这些直线会互相平行。

　　通过这个实验，密立根得到了一个普朗克常数的值，即6.57x1034Js，这与现在所广泛接受的普朗克常数值6.63x10-34Js也已经非常接近了。