考研概率论备考知识点及习题训练：边缘分布函数

   　考研概率论中的边缘分布函数是一个重要的概念，特别是在处理多元随机变量时。下面我将介绍边缘分布函数的定义、相关知识点以及一些习题供您训练。

　　定义及知识点

　　边缘分布函数

　　对于两个随机变量 X 和 Y 的联合分布函数 F(x,y)，边缘分布函数是指在其中一个变量固定时，另一个变量的分布函数。

　　对于 X 的边缘分布函数，记作 FX​(x)，其定义为：

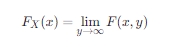
     或者等价地，通过积分联合概率密度函数得到：

     其中fX​(x)是X 的边缘概率密度函数。

　　对于 Y 的边缘分布函数，记作 FY​(y)，其定义为：

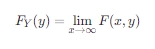
　　或者：

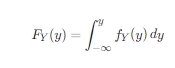
　　其中fY​(y)是Y 的边缘概率密度函数。

　　重要性质

　　边缘分布函数完全描述了一个随机变量自身的分布，而忽略了其他变量的信息。

　　边缘分布函数可以通过对联合分布函数进行积分得到。

　　习题训练

　　习题 1

　　假设随机变量 X 和 Y 的联合概率密度函数为 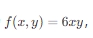，其中 。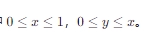

　　求出 X 的边缘概率密度函数 fX​(x)。

　　求出 Y 的边缘概率密度函数 fY​(y)。

　　习题 2

　　已知随机变量 X 和 Y 的联合分布函数为 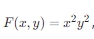，其中。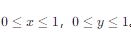

　　求 X 的边缘分布函数 FX​(x)。

　　求 Y 的边缘分布函数 FY​(y)。

　　习题 3

　　对于习题 1 中的随机变量 X 和 Y，求 。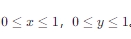

　　这些习题将帮助您更好地理解和应用边缘分布函数的概念。在解决这些问题时，请确保遵循概率论的基本原则和方法。如果您需要解答或者解释，请告诉我。

　新航道-用心用情用力做教育!

　　>>点击在线咨询<<

　　400-900-9767