考研线性代数知识点：行列式

   　行列式是线性代数中的一个重要概念，它在解决线性方程组、矩阵乘法、特征值等问题中具有重要作用。以下是一些关于行列式的考研重点知识点：

　　行列式的定义： 行列式是一个函数，它从 n \times nn×n 矩阵全体中取值，记作 \det(A)det(A) 或 |A|∣A∣，其中 AA 是一个 n \times nn×n 矩阵。

　　行列式的性质：

　　对换性质：行列式经过任意两行的对换，其值变号。

　　倍加性质：一行(列)的若干倍加到另一行(列)上，行列式的值不变。

　　行(列)变换性质：通过行(列)的初等行变换，行列式的值保持不变。

　　矩阵分块性质：行列式可以分解为子矩阵的行列式的乘积。

　　行列式的计算：

　　展开计算：行列式可以按照行或列展开计算，例如拉普拉斯展开、余子式展开等。

　　三角形矩阵：对角线以上的元素全为零的矩阵，其行列式等于对角线元素的乘积。

　　对角矩阵：所有非对角线元素都为零的矩阵，其行列式等于对角线元素的乘积。

　　行列式与线性方程组：

　　线性方程组有解当且仅当系数矩阵的行列式不为零。

　　线性方程组有无穷多解当且仅当系数矩阵的行列式为零。

　　行列式与矩阵的逆：

　　矩阵 AA 可逆当且仅当它的行列式不为零，且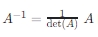

的伴随矩阵。

　　行列式与矩阵的特征值：

　　矩阵的特征多项式的常数项等于矩阵的行列式的相反数。

　　矩阵有零特征值当且仅当其行列式为零。

　　以上是行列式相关的部分重要知识点，掌握这些内容对于理解线性代数的其他部分至关重要，也是考研数学中的重点内容。希望对你有所帮助。

　新航道-用心用情用力做教育!

　　>>点击在线咨询<<

　　400-900-9767