考研线性代数重要基础知识点：向量

       考研线性代数中，向量是基础且重要的概念。以下是关于向量的几个关键知识点：

　　向量的定义：

　　向量是具有大小和方向的量，通常用粗体字母或者字母上加箭头表示，如。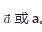

　　向量的表示：

　　坐标表示：在n维空间中，一个向量可以用一个n元组(a1, a2, …, an)表示，也可以用列矩阵的形式表示，如​​​。

　　基向量：在n维空间中，通常有一组基向量​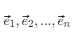,，任何一个向量都可以表示为基向量的线性组合。

　　向量的运算：

　　加法：两个向量相加，遵循分量的加法规则，即 。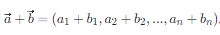

　　数乘：一个向量与一个标量相乘，遵循分量乘法规则，即 。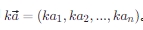

　　点积(内积)：两个向量的点积定义为​。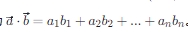

　　叉积(外积)：在三维空间中，两个向量的叉积是一个向量，其方向垂直于原来的两个向量。

　　向量的性质：

　　线性相关性：一组向量中，如果存在向量可以被其余向量线性表示，则称这组向量线性相关;否则，称它们线性无关。

　　长度(范数)：向量的长度通常用欧几里得范数表示，即。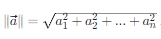

　　单位向量：长度为1的向量称为单位向量，可以通过将向量除以其长度得到。

　　向量的应用：

　　在线性代数中，向量空间、线性变换、特征值和特征向量等概念都与向量有着密切的关系。

　　掌握这些基础知识点对于理解线性代数的更深层次概念至关重要。在考研复习过程中，应该结合大量习题来巩固这些知识点。

　新航道-用心用情用力做教育!

　　>>点击在线咨询<<

　　400-900-9767