考研数学试卷中是如何考查多元函数极值的?

      考研数学试卷中，多元函数极值的考查通常涉及以下几个方面：

　　多元函数的极值概念：考查考生对多元函数极值定义的理解，包括局部极值、全局极值以及极值点的概念。

　　极值存在的条件：考查考生对多元函数极值必要条件和充分条件的掌握，尤其是拉格朗日乘数法和极值的二次判别法。

　　以下是一些具体的考查方式：

　　必要条件(费马定理的推广)

　　题目类型：给定一个多元函数，要求考生找出可能的极值点。

　　解题方法：利用偏导数，求出函数的驻点(即所有一阶偏导数为零的点)。

　　充分条件(二次判别法)

　　题目类型：给定一个多元函数及其在某点的二阶偏导数，要求判断该点是否为极值点，并确定是极大值还是极小值。

　　解题方法：计算二阶偏导数在该点的值，构造海森矩阵(Hessian矩阵)，并根据矩阵的正定性、负定性或不定性来判断极值类型。

　　拉格朗日乘数法

　　题目类型：在给定约束条件下，求多元函数的极值。

　　解题方法：构造拉格朗日函数(Lagrange function)，利用拉格朗日乘数法求解约束条件下的驻点，然后判断这些点是否为极值点。

　　以下是具体的例子：

　　例子1：必要条件

　　假设有函数 f(x,y)求其在点 (x0​,y0​) 处的极值，首先需要计算其一阶偏导数并令其为零：

　　例子2：充分条件

　　假设有函数 f(x,y) 在点 (x0​,y0​) 处的一阶偏导数为零，其二阶偏导数为：

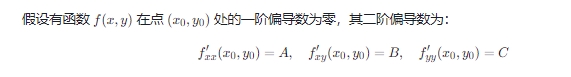
　　构造判别式 2AC−B2，根据其正负来判断：

　　例子3：拉格朗日乘数法

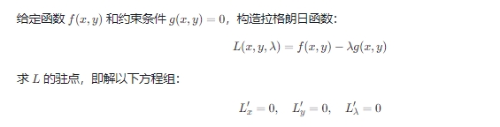
　　考研数学试卷在考查多元函数极值时，可能会结合不同的知识点，如线性代数中的行列式、矩阵的特征值等，来综合考查考生的数学分析能力。因此，考生需要熟练掌握相关理论，并能够灵活运用到具体问题的解决中。

　新航道-用心用情用力做教育!

　　>>点击在线咨询<<

　　400-900-9767