考研概率论与数理统计重要基础知识点：最值的分布

  　考研概率论与数理统计中的最值分布，主要指的是一组随机变量的值和最小值的概率分布。以下是关于最值分布的一些重要基础知识点：

     分值

　　设X1​,X2​,…,Xn​是相互独立的随机变量，它们的分布函数分别为FXi​​(x)，那么这组随机变量的值M=max(X1​,X2​,…,Xn​)的分布函数FM​(x)可以表示为：

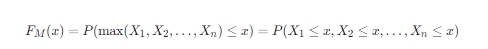
　　由于Xi​相互独立，所以有：

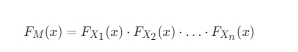
　　相应的概率密度函数fM​(x)可以通过对分布函数求导得到：

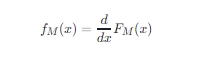
　　最小值分布

　　类似地，设X1​,X2​,…,Xn​是相互独立的随机变量，那么这组随机变量的最小值m=min(X1​,X2​,…,Xn​)的分布函数Fm​(x)可以表示为：

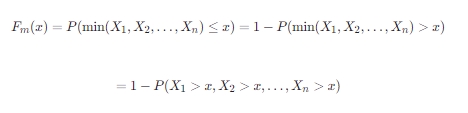
      类似地，设X1​,X2​,…,Xn​是相互独立的随机变量，那么这组随机变量的最小值m=min(X1​,X2​,…,Xn​)的分布函数Fm​(x)可以表示为：

　　由于Xi​相互独立，所以有：

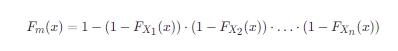
　　相应的概率密度函数fm​(x)可以通过对分布函数求导得到：

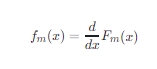
　　特点

　　独立性：上述方法适用于相互独立的随机变量。

　　连续性：上述推导适用于连续型随机变量。对于离散型随机变量，最值分布的推导略有不同。

　　计算：在实际计算中，通常需要知道各个Xi​的具体分布类型，才能进一步计算值或最小值的分布。

　　了解和掌握最值分布是考研概率论与数理统计部分的重要内容，对于解决实际问题非常有帮助。在备考过程中，应当结合具体例题来加深理解和运用。

　新航道-用心用情用力做教育!

　　>>点击在线咨询<<

　400-892-8866